FF
Overview
JARVIS-FF is a repository of classical force-field/potential calculation data intended to help users select the most appropriate force-field for a specific application. Many classical force-fields are developed for a particular set of properties (such as energies), and may not have been tested for properties not included in training (such as elastic constants, or defect formation energies). JARVIS-FF provides an automatic framework to consistently calculate and compare basic properties, such as the bulk modulus, defect formation energies, phonons, etc. that may be critical for specific molecular-dynamics simulations. JARVIS-FF relies on DFT and experimental data to evaluate accuracy.
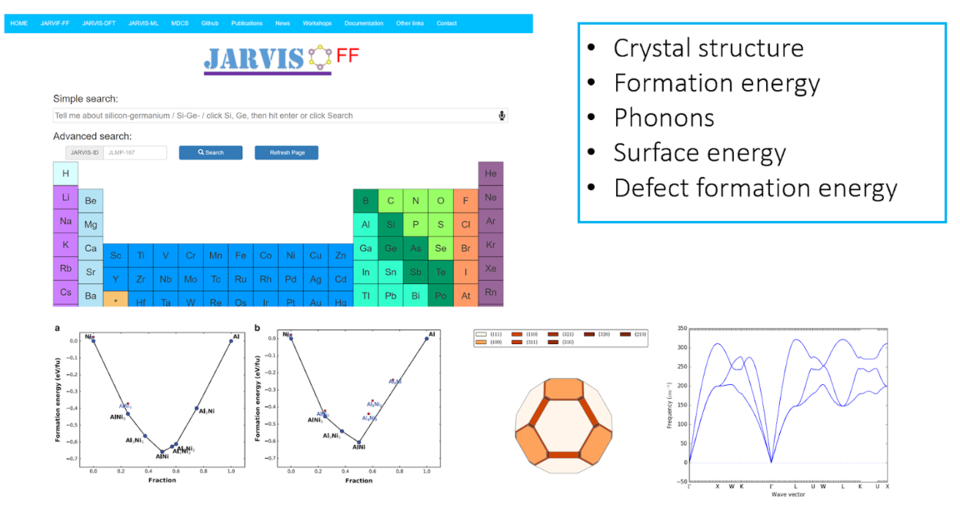
Table. A summary of various types of force-fields available in the JARVIS-FF.
| Force-fields | Numbers |
|---|---|
| EAM | 92 |
| Tersoff | 9 |
| ReaxFF | 5 |
| COMB | 6 |
| AIREBO | 2 |
| MEAM | 1 |
| EIM | 1 |
Methodology
- We started by downloading all the available potentials from the NIST interatomic potential repository (IPR) and from LAMMPS software directory.
- For each element having at least a potential, we downloaded all the corresponding crystal structures from the Materials Project or JARVIS-DFT database.
- We also downloaded all the energetics and mechanical properties data from and stored them in a separate database for a later comparison with the classical results (LAMMPS calculations at T=0 K).
- The high-throughput setting of LAMMPS jobs was done using JARVIS-tools.
- In our runs we used 10-06 as strain, 10-10 eV/Å for force convergence during the minimization to optimize
the structure and 1000 maximum iteration for structure optimization.
These are generalized computational set-up parameters, and the energetics and elastic constant data may or may not depend on them. - We tested strain parameters for a range of values (10-04, 10-06 and 10-08) but obviously evaluating such set of parameters for all the calculations was too extensive a work and was not carried out here.
- The relaxed structure was also stored along with the above files for later use such as for performing defect, phonon or other similar calculations. After the minimization, the crystal structure is stored in LAMMPS data-format and JSON format.
- Using this JSON file, unique Wyckoff positions were identified and deleted to represent vacancy-structures. The multiplicity of the Wyckoff positions is also recorded.
- After the defect structure generation, the LAMMPS energy minimization is carried out. In a subsequent run, we calculate the chemical potential of the defect element using the specific force-field.
- The data for the vacancy structure, chemical potential of element and perfect structure energy were used to calculate the defect formation energies. The most stable prototype for chemical potential calculation was determined using the energy above convex hull data from DFT. The defect structures were required to be at least 1.5 nm long in the x, y and z directions to avoid self-interactions with the periodic images of the simulation cell. Similar to the defect structures, distinct surfaces were created up to 3 Miller indices with the relaxed structure stored in the JSON file.
- A generic code for generating defect and surface structures is given at our github page. We enforce the surfaces to be at least 2.5 nm thick and with 2.5 nm vacuum in the simulation box. The 2.5 nm vacuum is used to ensure no self-interaction and the thickness is used to mimic actual experimental surface. Using the energies of perfect bulk and surface structures, surface energies for a specific plane are calculated.
- We should point out that only unreconstructed surfaces without any surface-segregation effects are computed, as our high-throughput approach does not allow for taking into account specific, element dependent reconstructions yet.
- Phonons were obtained by making an interface of JARVIS-FF with Phonopy package at 0 K. For deformed-structures, constant volume ensemble was used. The deformed structures were taken of at least 1.5 nm size in all directions.
from jarvis.tasks.lammps.lammps import LammpsJob, JobFactory
from jarvis.core.atoms import Atoms
atoms = Atoms.from_cif('abc.cif')
parameters = {
"pair_style": "eam/alloy",
"pair_coeff": "/data/knc6/JARVIS-FF-NEW/FS/Al1.eam.fs",
"atom_style": "charge",
"control_file": "inelast.mod",
}
lmp = LammpsJob(atoms=atoms, parameters=parameters, lammps_cmd=cmd).runjob()
job_fact = JobFactory(pair_style='eam/alloy',name="my_first_lammps_run")
cmd = 'lmp_serial<in.main>lmp.out'
job_fact.all_props_eam_alloy(atoms=atoms,ff_path='Al1.eam.fs',lammps_cmd=cmd)
Property details and assesment
- Using jarvis.core.Atoms class several atomistic properties such as lattice parameters, density, packing fraction etc. can be calculated.
- The optimized lattice parameters generally compare well with DFT data except for the FFs where a particular phase was not trained during FF-fitting.
- Similarly, energetics in terms of convex hull plot is compared between DFT and FF results.
- Elastic tensor and derived properties were predicted using LAMMPS runs and comapred with DFT data.
- For the defect formation energies, we consider vacancies and free-surfaces which are generated by the modules in the JARVIS-Tools.
- Phonon data from JARVIS-DFT and JARVIS-FF can be compared for a system to evaluate the phonon quality. However, it is important to note that in DFT there might be only conventional cell Gamma-point phonon data available whereas in JARVIS-FF we use supercell finite difference-based approach for obtaining phonon density of states and bandstructures.
- For a known stable material if the phonon bandstructure shows high negative values then it signifies the FF maynot be suitable to predict correct dynamical properties of the system.